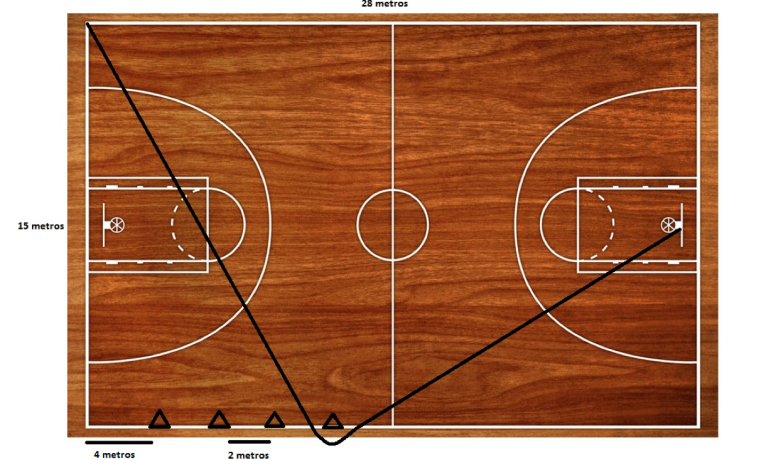
LEMA es un proyecto financiado por la Unión Europea, desarrollado entre el año 2006 y 2009, cuyo objetivo es incluir las actividades de modelizaciónn en la enseñananza de las matemáticas. A partir de un determinado contexto, lo que denominan “la situación”, se proponen varias preguntas relacionadas, que deben ser resueltas en pequeños grupos de trabajo, durante una o dos sesiones de trabajo.
Extraído de : Modelización matemática en la educación secundaria: manual de uso. Modelling in Science Education and Learning. Volume 12 (1), 2019